※For a shorter version, go to “Wettability (Wenzel’s equation)”.
Intrinsic Wetting Threshold
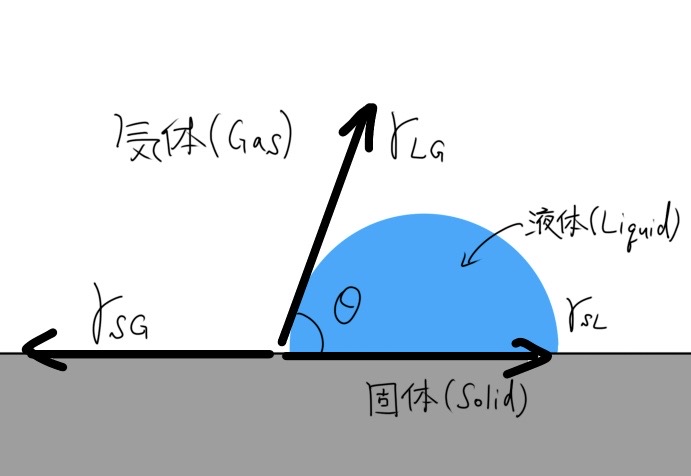
In “Interface Physics 〜1.Young’s equation〜”, we discussed Young’s equation.
(Please click here if you haven’t read it yet)
This is an equation that introduced the concept of Contact Angle (CA), which allowed for a quantitative expression of how much a droplet would spread over a solid surface.
In the previous article, we wrote that when the contact angle θ is greater than 90 degrees, it is called “hydrophobic” and when it is less than 90 degrees, it is called “hydrophilic”, but recent experimental results differ slightly from this theory.
According to actual research, the contact angle θ of a water droplet, which distinguishes between “hydrophobic” and “hydrophilic”, is reported to be 65 degrees [1].
This boundary angle has its own unique value in water and other liquids, which is called the Intrinsic Wetting Threshold (IWT) [2].
Especially in the case of water, its IWT can be expressed as $$\theta_{IWT} = 65°.$$
(Furthermore, it has been reported that the lower the surface tension of the liquid, the smaller the IWT [3].)
In addition, surface free energy and surface tension (γSG) determine the basic wettability and surface properties of the material, i.e., hydrophilicity/hydrophobicity. Specifically, the larger the value of $$\gamma_{SG},$$
the more hydrophilic the surface, while the smaller the surface, the more hydrophobic it is. (Fig. S1).
So, how can we control the wettability of a surface?
Broadly speaking, there are two types of surface modification:
【1】 modification by chemical materials (chemical method) and
【2】 modification by surface roughness (physical method).
A typical example of 【1】 is the Teflon coating on a frying pan (Fig. 1).

In this article, we will look at 【2】in detail while introducing Wenzel’s equation.
Wettability (Wenzel’s equation)
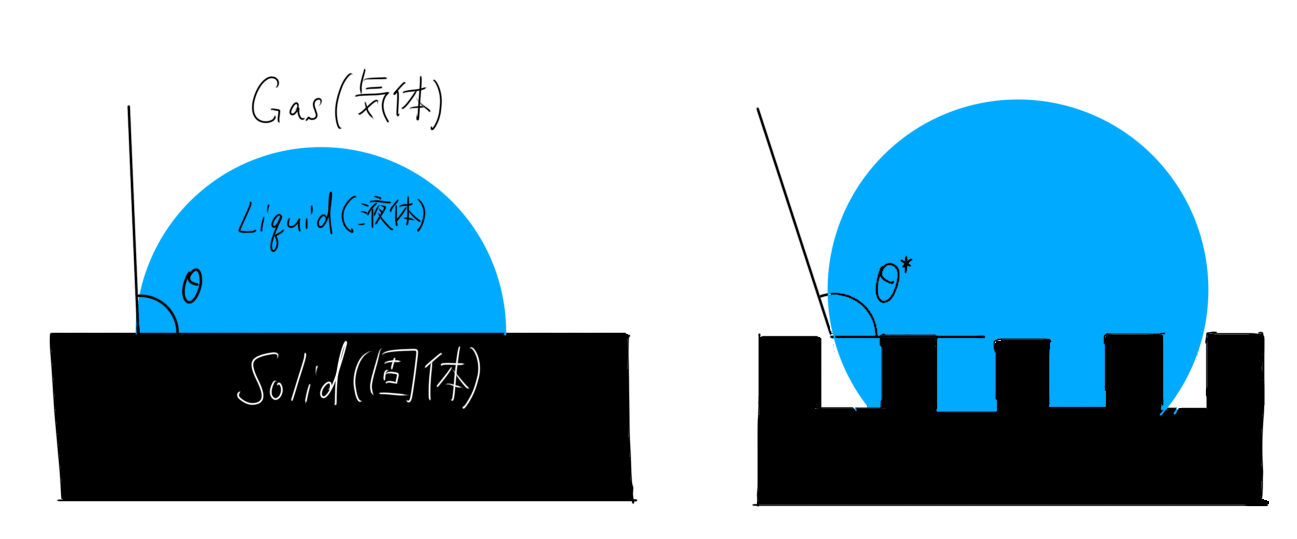
Surface roughness is important in improving surface wettability. Now let’s consider a surface that is R times rougher than the flat surface we previously considered.
The relationship between the contact angle and surface roughness can be expressed as
$$\cos\theta^{*} = R\cos\theta,$$
which is called the Wenzel equation. Here, $$\theta^{*}, R, \theta$$ are the apparent contact angle, surface roughness, and contact angle, respectively.
Compare the figures representing the Wenzel equation and Young’s equation in Fig. 2 to see the difference.
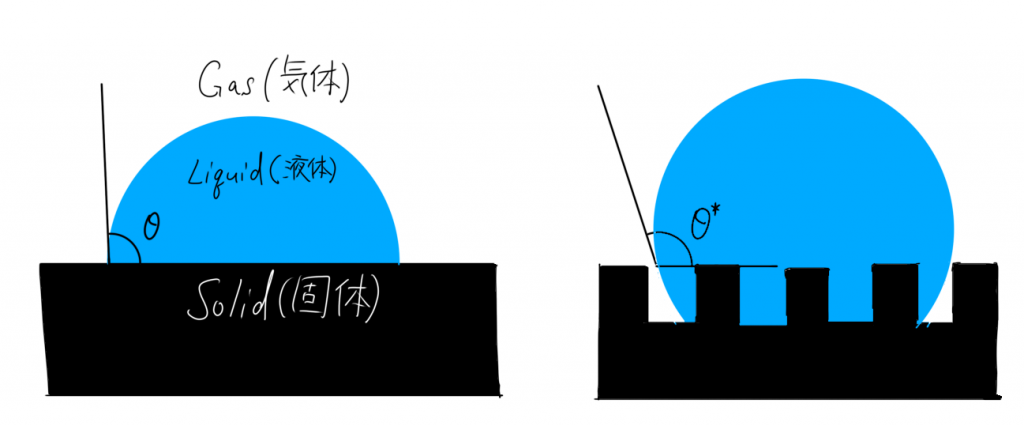
In the case of water droplets, you can see that the rough surface is more hydrophobic.
That is, as the surface roughness increases, the hydrophilic surface becomes more hydrophilic and the hydrophobic surface becomes more hydrophobic [4]. In other words, the roughness emphasizes the inherent “wettability” of the product.
By physically modifying the surface in this way, superhydrophobic and superhydrophilic properties can be developed.
In this article, we explained Wenzel’s equation. By using this equation, we can describe a uniform surface. However, there are many non-uniform surfaces in the world where Wenzel’s equation cannot be applied.
Next time, we’ll extend the Wenzel’s model to delve deeper into wettability on heterogeneous surfaces.
The Principia-Lab Team
Reference
[1] Stimuli-Responsive Bioinspired Materials for Controllable Liquid Manipulation: Principles, Fabrication, and Applications.
[2] Bioinspired Designs of Superhydrophobic and Superhydrophilic Materials.
[3] A General Strategy for the Separation of Immiscible Organic Liquids by Manipulating the Surface Tensions of Nanofibrous Membranes.
[4] Some thoughts on superhydrophobic wetting.