界面物理学〜2.Wenzelの式〜

※ざっくりと読みたい方は「濡れ性（Wenzelの式）」から。

濡れ閾値（Intrinsic Wetting Threshold）

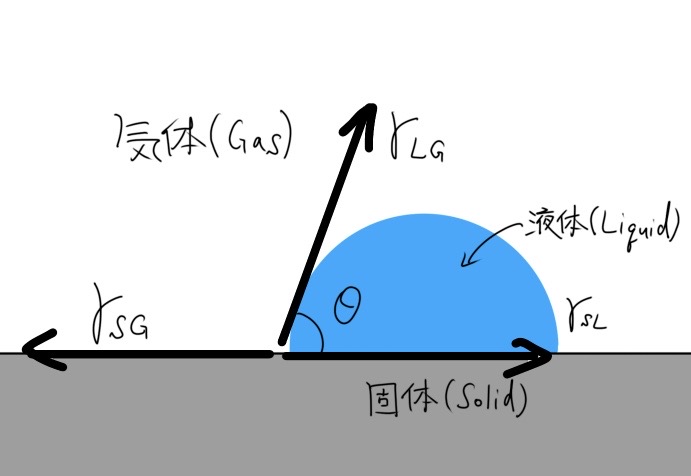
界面物理学〜1.Youngの式〜では、Youngの式について説明しました。(まだ読んでない方はこちら)

これは、接触角(Contact Angle)という概念を導入して、液滴が固体表面にどれくらい濡れ広がるかを定量的に表すことができる式でした。

前回の記事では、接触角θの値が90度よりも大きいと「撥水性」、90度よりも小さいと「親水性」と呼ばれると書きましたが、近年の実験結果では、この理論と少し異なります。

実際の研究結果によると、「撥水性」と「親水性」を区別する水滴の接触角θは、90度よりも小さいとされており、文献では、65度と報告されています[1]。

この境界となる角度は、水やその他の液体において、それぞれ固有の値を持っており、濡れ閾値(Intrinsic Wetting Threshold)と呼ばれます[2]。

水の場合は、65度なので、$$\theta_{IWT} = 65°$$と表せますね。
（さらに、表面張力が低い液体ほど、IWTが小さいと報告されています[3]。）

また、表面自由エネルギーや表面張力（γ_SG）は、材料表面の基本的な濡れ性や表面特性、つまり、親液性/疎液性を決定します。具体的には、$$\gamma_{SG}$$の値が大きいほど親液性になり、小さいほど疎液性の表面となります。(図S1)

では、この表面の濡れ性はどうやってコントロールできるのでしょうか？

大きく分けると、
【1】化学材料を表面に修飾する(化学的手法)
【2】表面に凹凸をつける(物理的手法)
の二つがあります。

【1】の日常的な代表例としては、フライパンのテフロンコーティングなどが挙げられます(図1)。

今回は、Wenzelの式を紹介しながら、【2】について詳しく見ていきます。

表面の粗さは表面の濡れ性を改善する上で重要です。ここで、前回考えた平らな表面よりもR倍粗い表面を考えてみましょう。

この時、接触角と表面粗さの関係は、

$$\cos\theta^{*} = R\cos\theta$$

と表せ、これをWenzelの式といいます。ここで、$$\theta^{*}, R, \theta$$は、それぞれ、見かけの接触角、表面の粗さ、接触角です。

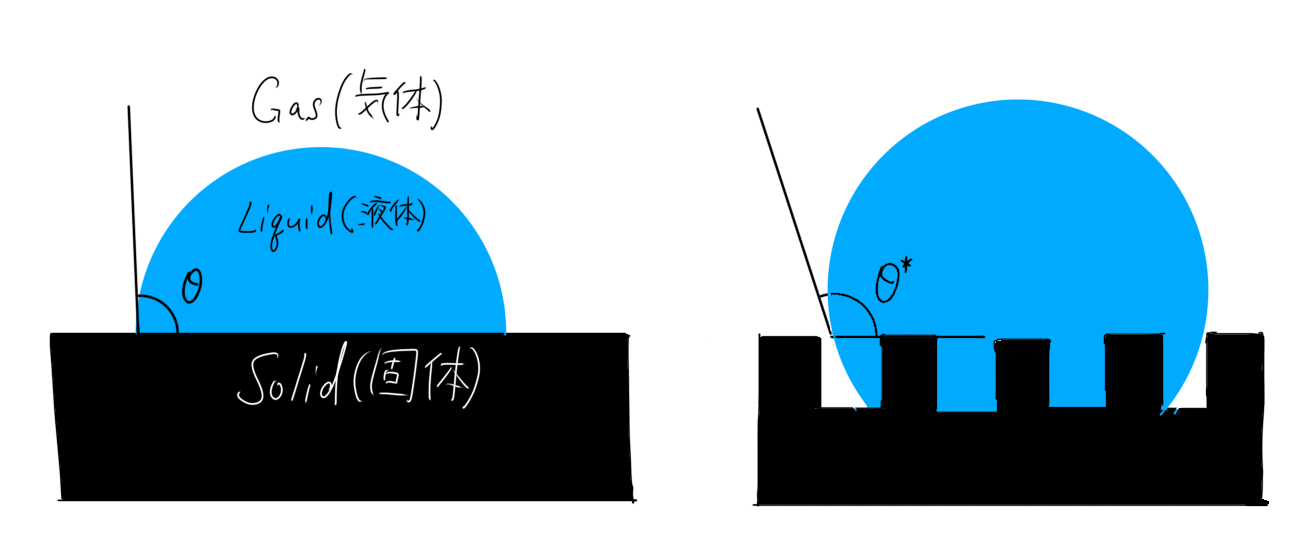
イメージが湧きやすいように、Youngの式の時に使った図と並べてみると図2のようになります。

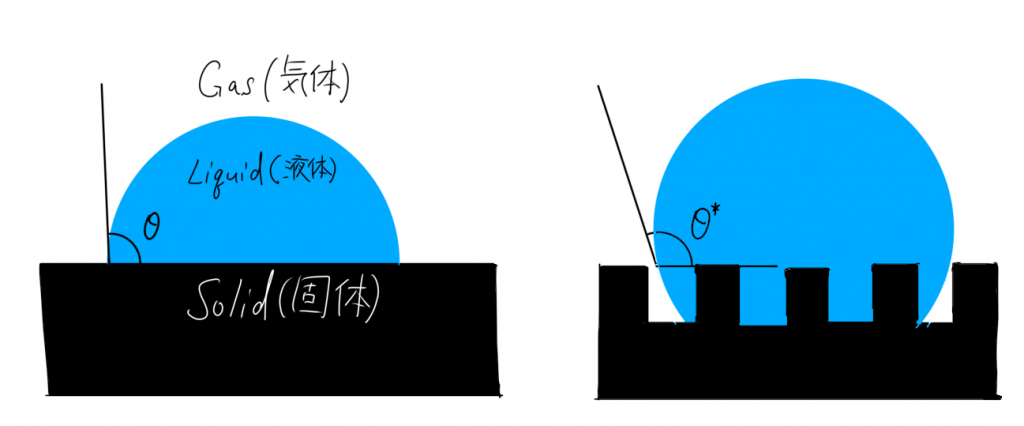
水滴の場合、凹凸表面だと、より撥水性になっていることが確認できますね。

つまり、表面の粗さが大きくなるにつれて、親液性表面はより親液性になり、疎液性表面はより疎液性になります[4]。言い換えると、本来備えている「濡れ性」が強調されるということになります。

このように物理的に表面を改良することで、超撥水性や超親水性を発現させることができるのです。

今回はWenzelの式に関して説明しました。この式を用いることで、均一な表面は説明できますが、世の中には不均一な表面も多数存在します。

次回の界面物理学では、Wenzelモデルを深掘りして、不均一表面での濡れ性に関して、深掘りしていきたいと思います。

プリンキピアラボチーム