Interface Physics 〜3.Cassie-Baxter equation〜

Non-uniform rough surface

In “Interface Physics 〜2.Wenzel’s equation〜”, we discussed Wenzel’s equation.

(Please click here for “Interface Physics 〜2.Wenzel’s equation〜” )

The equation describes the inherent “wettability” gets emphasized as the surface roughness (degree of unevenness) increases.

(If the surface is flat, you can use the Young’s equation to explain the wettability.)

Wenzel’s equation can explain a uniform rough surface, but there are also non-uniform surfaces that consist of two or more types of substances (Fig.1).

Figure 1. Example of non-uniform surface (mosaic surface).

Let’s schematically represent a cross section of such a substance (Fig. 2).

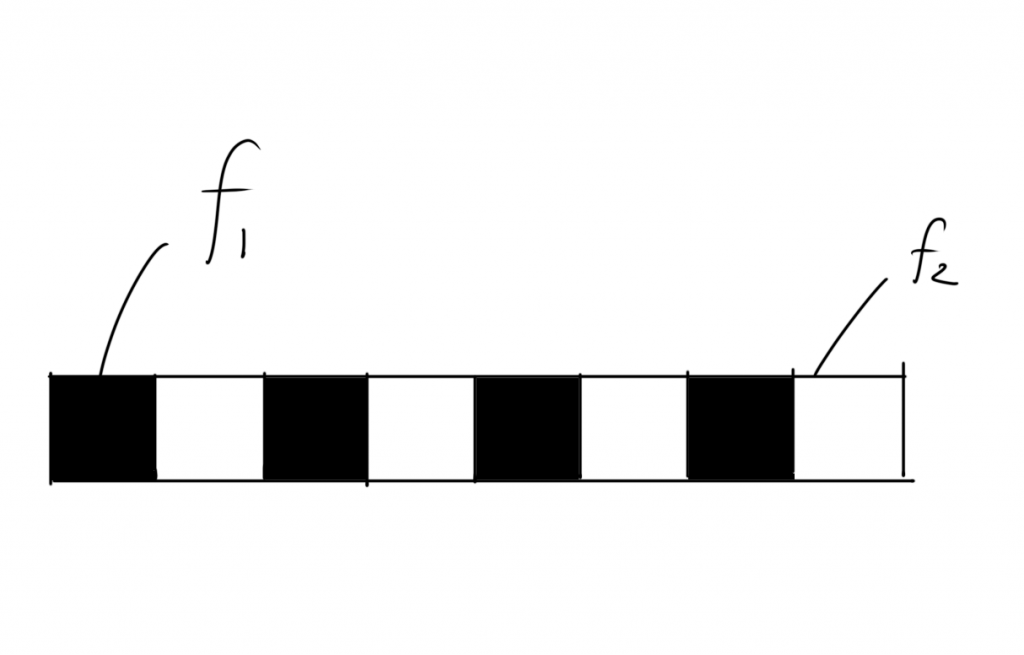
Figure 2. Schematic of non-uniform surface.

Here, f1,f2 are the area fractions of black and white substances on the solid surface, and has the condition, f1 + f2 = 1.

Thus, considering that a non-uniform surface is composed of two fine substances, the Cassie-Baxter equation can be applied. We will discuss this in the next section.

Wettability (Cassie-Baxter equation )

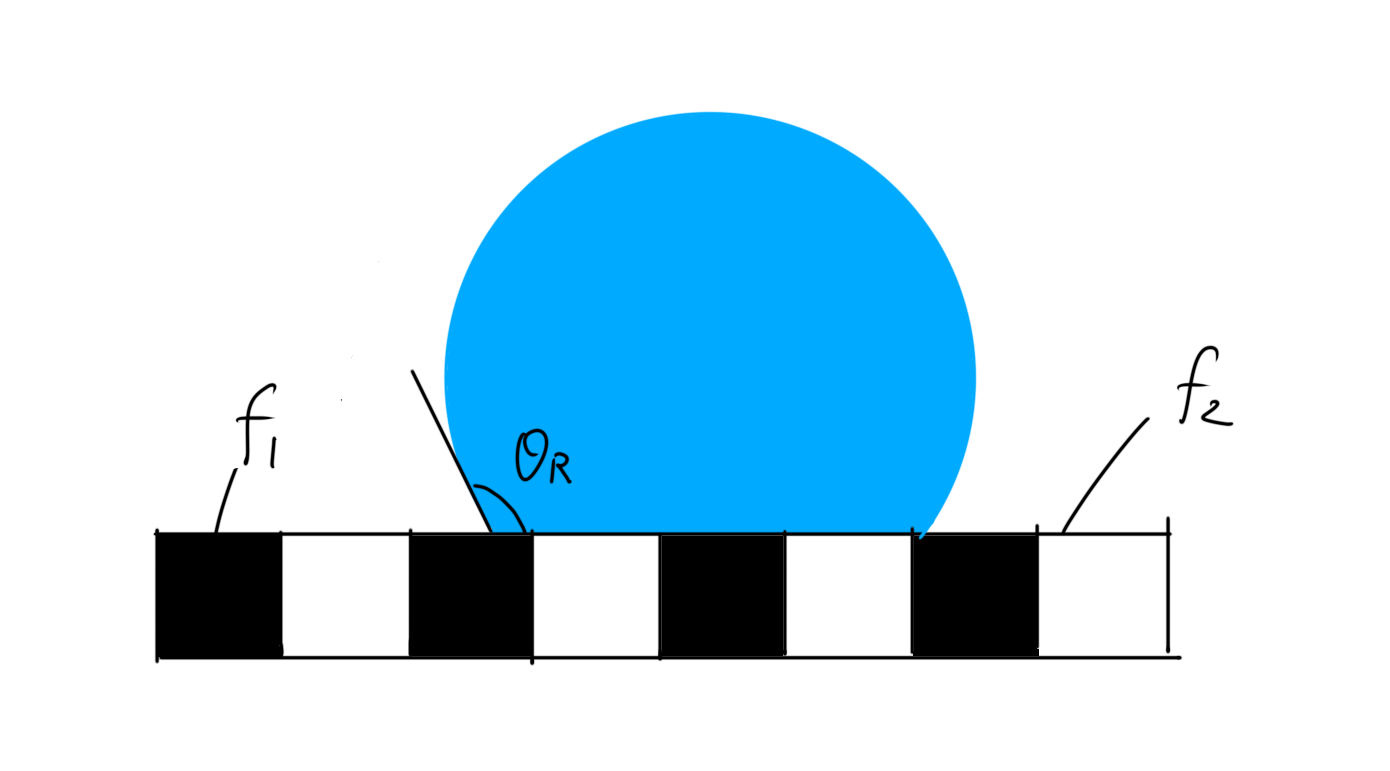
Let’s consider the contact angle when water drops are on the non-uniform surface shown in Fig. 2 (Fig. 3).

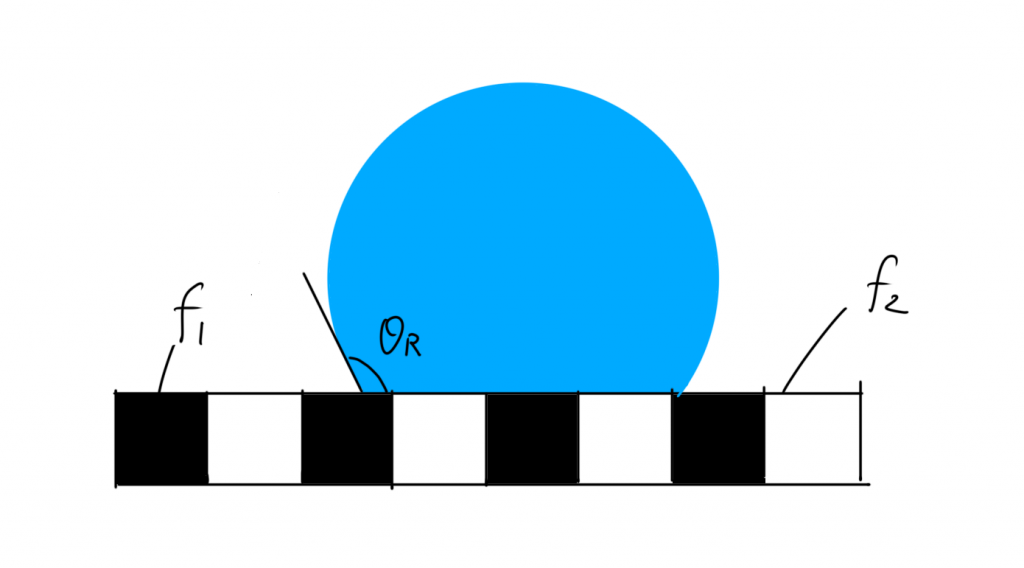
Figure 3. Water droplets on a non-uniform surface.

If the pure contact angles of black and white substances are θ1,θ2, the contact angle θR of a non-uniform surface is

$$\cos\theta_R = f_1\cos\theta_1+f_2\cos\theta_2 .$$

This is called the Cassie-Baxter equation [1,2].

Here, consider the white substance as “air”. Since θ2 = 180°, f1 + f2 = 1, the above equation is

$$\cos\theta_R =(f_1-1)+f_1\cos\theta_1 .$$

From this equation, it can be seen that the smaller f1 (i.e. the larger the area fraction occupied by air), the larger the contact angle θR , making the substance closer to hydrophobicity (Fig. 4).

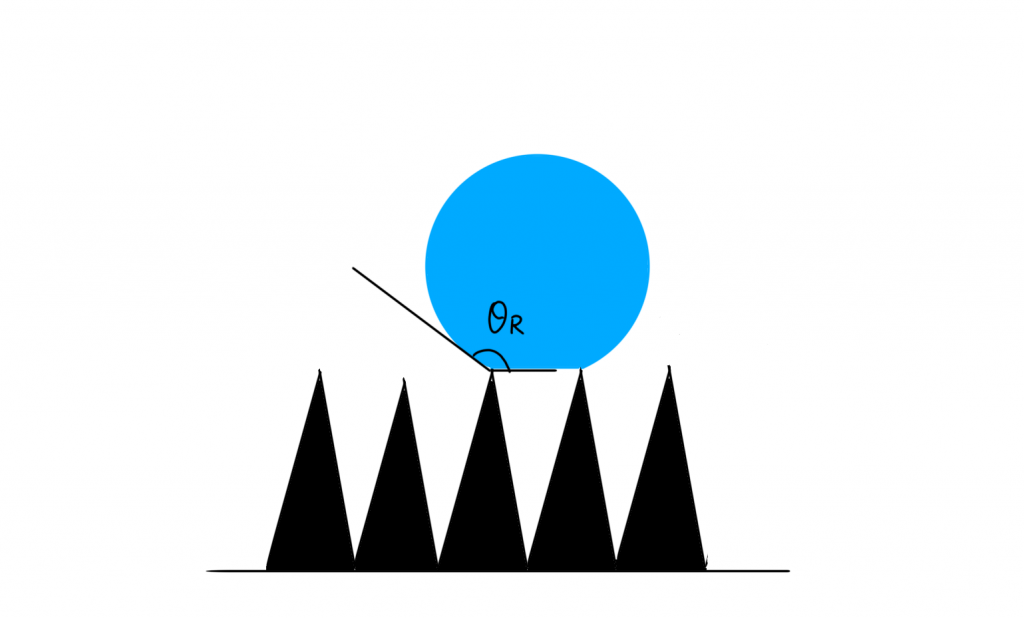
Figure 4. Droplet on non-uniform surface (when f1 is small).

Conversely, what happens if the area fraction of air is zero (f2 = 0)?

The contact angle θR can be expressed as

$$\cos\theta_R = f_1\cos\theta_1 .$$

As you may have noticed, this equation is the same as Wenzel’s equation (Fig. S1)

$$\cos\theta^{*} = R\cos\theta .$$

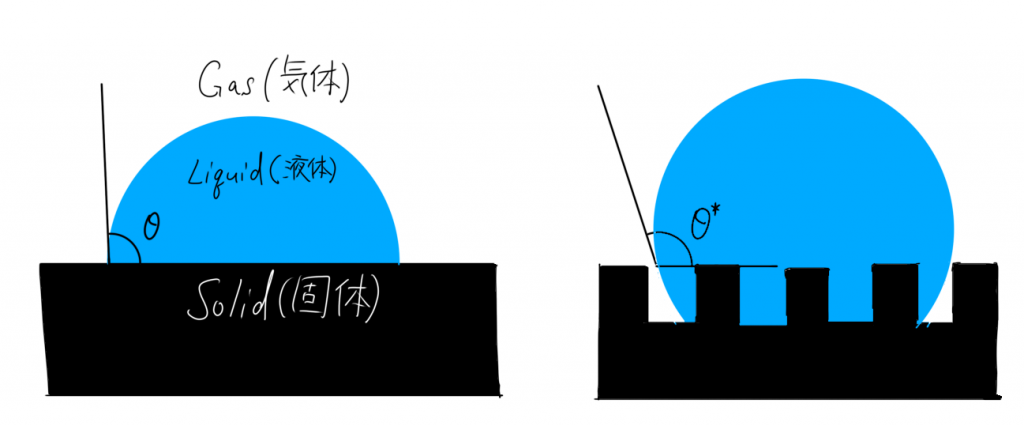
Figure S1. Young’s model (left) and Wenzel’s model (right).

Therefore, the Wenzel’s equation represents a special state of the Cassie–Baxter equation.

To summarize this chapter, we explained the Cassie-Baxter equation. By applying the three equations introduced so far, we can investigate the wettability of any solid surface that exists.

Next time, we would like to introduce plants and animals that have interesting surface structures related to wettability.

The Principia-Lab Team

Reference
[1] Stimuli-Responsive Bioinspired Materials for Controllable Liquid Manipulation: Principles, Fabrication, and Applications.
[2] WETTABILITY OF POROUS SURFACES.

Share: