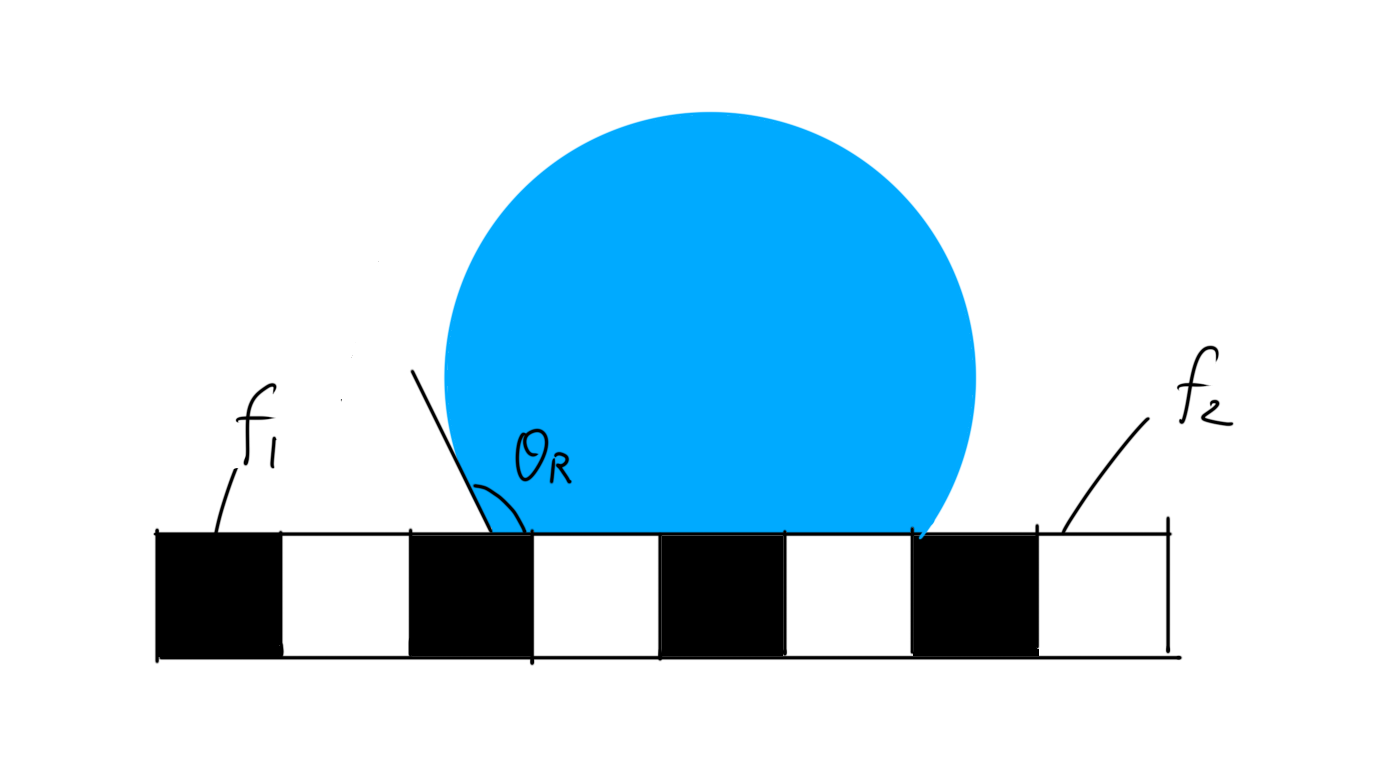
界面物理学〜3.Cassie-Baxterの式〜 - Principia Lab (プリンキピアラボ)

不均一な凹凸表面

界面物理学〜2.Wenzelの式〜では、Wenzelの式について説明しました。

(まだ読んでない方はこちら)

これは、表面の粗さ(凹凸度合い)が大きくなるにつれて、本来備えている「濡れ性」が強調されるということを表す式でした。

（表面が平らな場合は、濡れ性をYoungの式で説明できましたね。）

Wenzelの式は、均一な凹凸表面は説明できますが、世の中には、二種類以上の物質によって成り立つような不均一な表面も存在します(図1)。

このような物質の断面を模式的に表してみましょう(図2)。

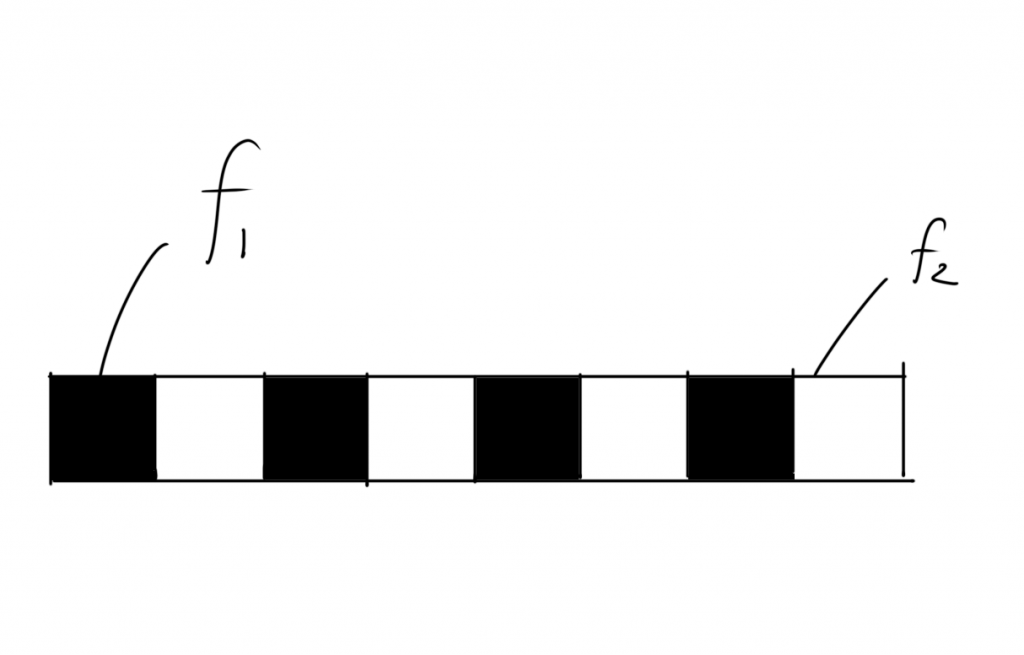
ここで、 f₁,f₂は、固体表面上で、黒色,白色の物質が占める面積分率で、 f₁ + f₂ = 1となります。

このように、不均一な表面は、微細な二種類の物質によって成り立つと考えると、Cassie-Baxterの式を適用できるようになります。次のセクションで解説していきます。

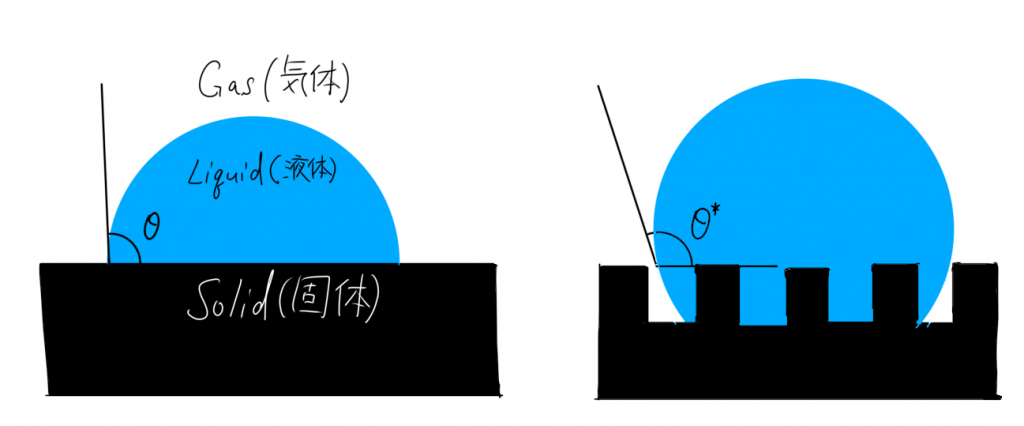
先ほど図2で示した不均一表面に、水滴が乗っている時の接触角を考えてみます(図3)。

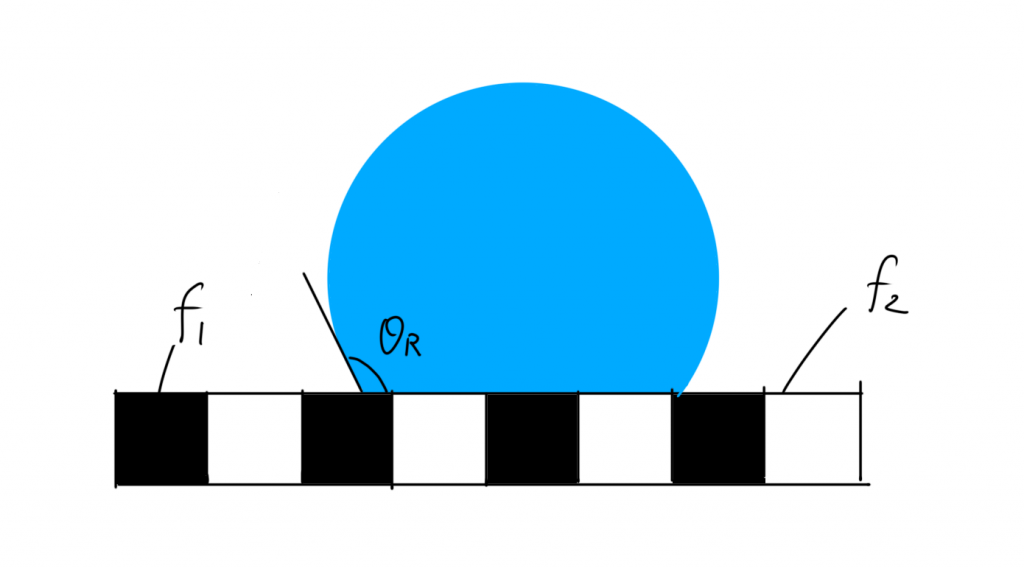
黒色,白色の物質の純粋な接触角をθ₁,θ₂だとすると、不均一表面における接触角θ_Rは、

$$\cos\theta_R = f_1\cos\theta_1+f_2\cos\theta_2$$

と表すことができます。これをCassie-Baxterの式といいます[1,2]。

ここで、白色の物質を「空気」とみなしてみると、先ほどの式は、θ₂ = 180°, f₁ + f₂ = 1より、

$$\cos\theta_R =(f_1-1)+f_1\cos\theta_1$$

と書き換えることができます。この式から、f₁が小さければ小さいほど、つまり空気の占める面積分率が大きいほど、接触角θ_Rが大きくなって、撥水性に近づいていくことが分かります(図4)。

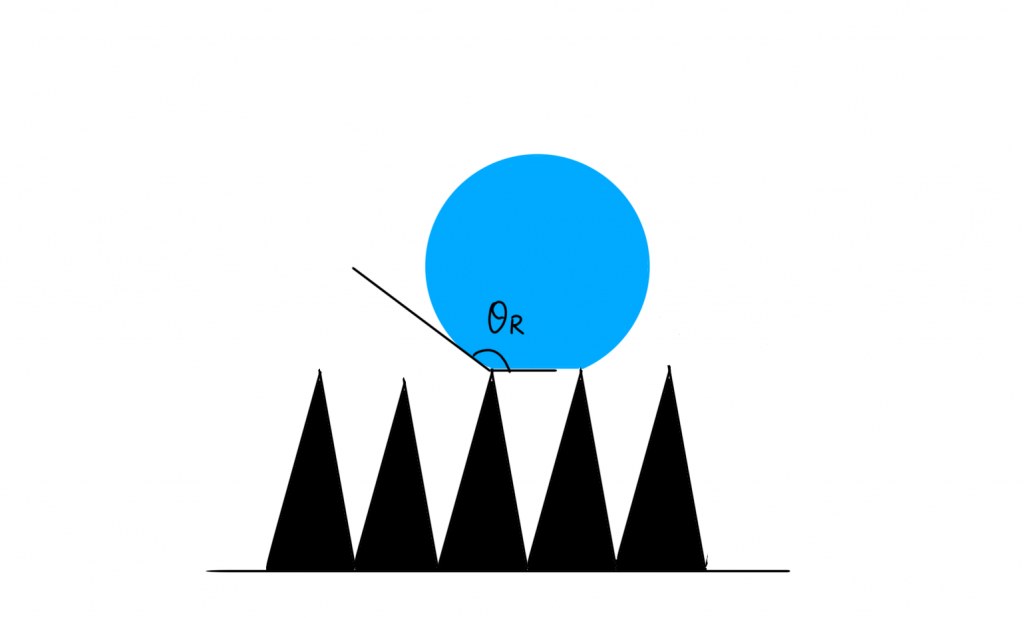
反対に、空気の占める面積分率がゼロの場合(f₂ = 0)、どうなるでしょうか？

先ほどの接触角θ_Rは、

$$\cos\theta_R = f_1\cos\theta_1$$

と表せます。もうお気づきかもしれませんが、この式は、前回のWenzelの式

$$\cos\theta^{*} = R\cos\theta$$

と一緒です(図S1)。

つまり、 Wenzel式というのは、Cassie–Baxterの式の特殊な状態を表しているのです。

さて、今回は、Cassie–Baxterの式を解説しました。今までに紹介した3つの式を応用すれば、世の中にあるあらゆる固体表面の濡れ性を調べることができます。

次回は、濡れ性と関係する、興味深い表面構造を持つ植物や動物について紹介していきたいと思います。

プリンキピアラボチーム